Models
represent reality.
Models constructed for different
purposes represent different aspects of
reality but no model represents every aspect.
All models simplify reality in some way. Model
airplanes may look like real planes but can’t fly,
others fly but don’t look real and wind tunnel
planes act like real planes and still can’t
fly. The model we use depends
on what we need
it to do.
Mathematical models
capture aspects of reality with equations.
The mathematical model
5 – 1 = 4
represents
a boy with five apples
who ate one and the same model
could represent many other things.
Complex models represent complex
ideas and everything rests on
assumptions about how
the world works.
Iterative mathematical models
represent situations in which some
quantitative process is repeated over and
over again, in a loop, and we want to know
how the consequences of that process develop
over time. The iterative mathematical model
below is general in the sense that it can represent
any number of situations. It represents a
girl with some number of apples who
ate some number each day until
they were gone and we want
to know how long
that took.
Apples = 10
Days = 0
Ration = 1 apple each day
Start eating
Apples = Apples – Ration
if (Apples > 0)
Apples = Apples – Ration
Days = Days + 1
go to Start Eating
if (Apples = 0)
go to Stop Eating
Stop Eating
Print Days
The answer
depends on the number
of apples at the start, the ration,
whether she ate apples every day, varied
the ration from day to day, or a horse ate
the rest of her apples. All of this would
be easy to model with the same basic
iterative structure, no matter
the details.
If the model
were complex enough or
needed many iterations ‘through
the ‘day loop’, it would be easier, faster,
and more reliable to run it on a computer
than to do it by hand. Computers are
fast, good at keeping track of
things, and usually don’t
make mistakes unless
you tell them to.
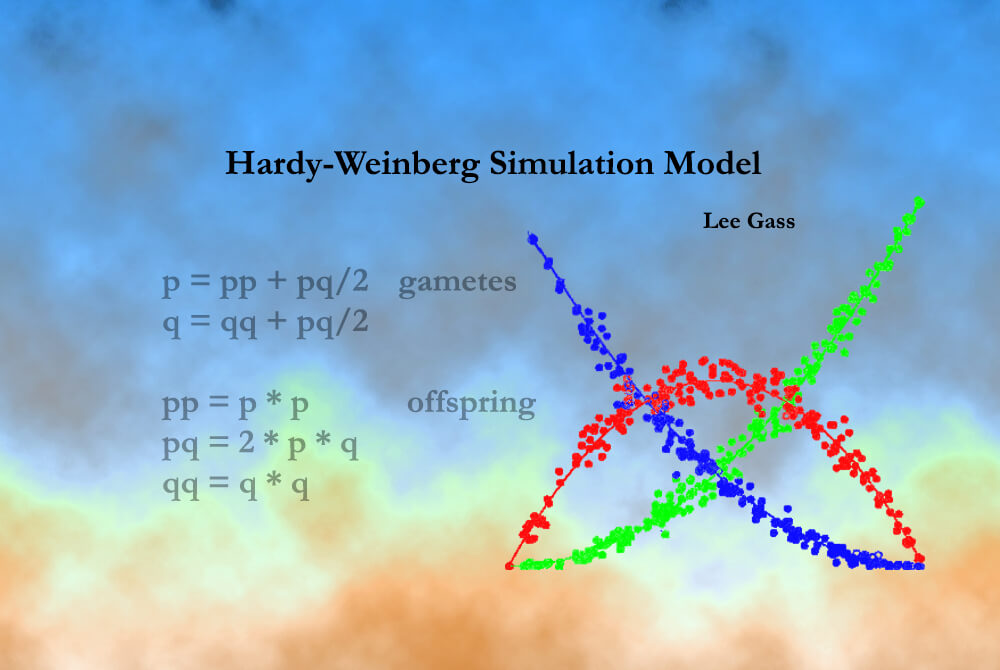
Hardy-Weinberg
Genetic Equilibrium Theory
allows us to predict the genetic
composition of populations over time, given
certain assumptions about migration, mutation rates,
mating patterns, population size and natural selection
– – mainly that none of them are changing. As long
as those ideal assumptions are met, the model
predicts that genetic structure remains
constant from generation
to generation.
According
to the theory, allele
frequencies in gene pools
and genotype frequencies in
populations remain constant if there
are no natural selection, mutation, or
migration, etc. We know the real world
is not constant in these ways, so the value of
the theory is not to show the real world is not
ideal. We already know that. The value of the
theory, as of theories in general, is to help us
understand how the real world differs
from the imaginary worlds
theories represent.
In this case,
Hardy-Weinberg Theory
helps us understand how the genetic
structure of populations changes over time
in response to specific selection pressures. The
theory’s predictions provide a yardstick and help
us see where, how, and whether the real world
violates those simple assumptions and shows
where the assumptions are wrong. You specify
the starting point and the selection pressures
and predict what will happen, given the
rest of the assumptions. The model
shows you whether
it would do
that.
What a way to learn!
It’s fast,
easy, fun, and tests your
knowledge of genetics and population
genetics to the core. Do it by yourself, do it
in groups, but do it. I’ll surely be doing it while
I wonder what to ask you on the final. Could I be
any clearer about how much I think using this model
will help you do well in this course? Anyone who
bet against my giving you an opportunity to
shine in genetics, population genetics, and
natural selection on the final could
not have been sitting in your
seat all year, because
you know better.
The Hardy-Weinberg
Simulation Model is an iterative, looping,
computer-based mathematical model of population
genetics using the Hardy-Weinberg equations
to model changes in a population under
conditions of natural selection
that you specify.
The model
is easy to run. When you
run it, it asks you for two kinds of
information about a simple, imaginary,
2 allele, 1 gene locus genetic system. It wants to
know the genotype frequencies at time zero for
the 3 possible genotypes, pp, pq, and qq, which are
the proportions of the 3 genotypes in the population.
The 3 values must sum to 1, or 100% of the genes
in the population for that locus, and they must
be in the proportions specified by
the binomial equation,
p2 + 2pq + p2 = 1.
(Try a different ratio and see what happens.)
Genotypes
are what genes you have.
Phenotpes are the way you are, and
to the extent that how you are is inherited
genetically, phenotypes reflect genotypes. The
model also needs to know selection pressures
against phenotypes, expressed as mortality rates.
What proportion of each phenotype dies each generation
without reproducing? If the p allele is dominant over
q, pp and pq have the same phenotype, the same
exposure to natural selection, and the same
mortality rates but if neither dominates
the other they are different
phenotypically.
So when you
assign mortality rates, you
are also deciding whether the genetic
systems you investigate involve dominance,
which is one of the things those numbers mean.
If neither allele dominates, there are 3 phenotypes,
3 exposures to natural selection, 3 mortalities, and
a different outcome of the model. You could predict
that simple result from your understanding of
simple Mendelian genetics without running
the model, but test the prediction with
the model to be sure you
understand it.
There is much
more to be learned with
the model, though. Some results
will confirm your understanding but
some will surprise you, stop you, and make
you scratch your head for a while. Then
try this, that, and the other thing
with the model until you
understand it.
The test of your understanding
is the accuracy of your predictions,
so don’t skip that essential step.
Using those
simple parameters, the model
iterates through the Hardy-Weinberg
equations to predict 50 generations of changes
in the genetic composition of the population you
define and illustrates the results as graphs and
tables of numbers. Before I turn you loose
to play with the model you need to
understand how it works.
It’s simple.
When you
click to run the program,
you get a page of numbers and
those at the top are all you need
to know for now. There are
exactly six of them. You
need to understand
all six.
Lines 1 to
3 are the proportions of
each phenotype in the population
dying before reproducing each generation,
the mortality rates that estimate the power
of natural selection to shape gene pools. You can
change any of those numbers, as you like. Note that
unless you change it, the model assumes 10% of pp
genotypes die before reproducing each generation, and
100% of other 2 genotypes survive and reproduce. There
is no magic in that starting point, other than that it should
be interesting to you genetically. Basically, the model
must start somewhere, and that’s it. It’s up to you to
use it as a tool. Its value is in how you set it up,
which depends on what you want to know.
That depends on what you don’t know
– – your ignorance. Working the
model is a great way to
learn what you
know.
In addition
to mortality rates, you
can change starting conditions,
or the pp’s and qq’s that define populations
and gene pools. You’ll set those at time zero
(generation 0, line 7), which is how and
when things start out. How they change
depends on the selection pressures
that you impose through
mortality rates.
If you
don’t know how to
calculate p’s and q’s from
pp’s, pq’s, and qq’s, don’t worry
about it at first. Excel will fix it for
you, but the first generation of your
graphs will take a jump. Learn to do
it yourself, save Excel the trouble,
and your graphs will be more
beautiful and more useful
learning tools.
After you
set those 6 numbers,
Excel calculates the rest of
the values automatically with Hardy
-Weinberg math, all 50 generations in a
heartbeat, and draws all the graphs for you,
just from those six numbers. You could do it
yourself by hand if you needed to, and please
don’t think you won’t get a chance to demon-
strate that ability on the final, but having
Excel turn the crank for you saves
tons of time learning and helps you
learn much more deeply and
remember it longer
as well.
To run the
Hardy Weinberg Simulation
Model, Microsoft Excel must be on your
computer (it is part of MS Office).
If so, just click HWSim.
Set the 6
numbers and
look at the results.
—————————
Selection against pp (ppMort)?
Selection against pq (pqMort)?
Selection against qq (qqMort)?
—————————————
Frequency of pp in the population?
Frequency of pq in the population?
Frequency of qq in the population?
——————————————-
Excel calculates everything automatically.
Here’s how the model would work if
you were turning its crank by hand
Calculate survival rates
from mortality rates.
ppSurv = 1 – ppMort
pqSurv = 1 – pqMort
qqSurv = 1 – qqMort
Enter Generation Loop
Gen = 0
Start Generation Loop
Apply mortality
pp = pp * ppSurv
pq = pq * pqSurv
qq = qq * qqSurv
Calculate post-mortality genetics.
SumSurv = pp + pq + qq
pp = pp/SumSurv
pq = pq/SumSurv
qq = qq/SumSurv
p = pp + pq/2
q = qq + pq/2
Calculate offspring genetics
pp = p * p
pq = p * q * 2
qq = q * q
Save genetics: pp, pq, qq, p, q
Administer Generation Loop
if (Gen < 50)
Gen = Gen + 1
go to Enter Generation Loop
if (Gen = 50)
go to Stop Looping
Stop Looping
Draw graphs
Stop
Then study the results,
think about what they tell you,
realize what you still need to know,
and do everything again until you know
what you need to know to understand
how natural selection works in
natural and modeled systems.
——————–
In the
example, Excel
assumes that unless you
change things, the homozygous pp
phenotype suffers 10% pre-reproduction
mortality each generation, compared
to the others, which get off Scot free.
—————————————
The Allele Frequency Chart
(the tab at the table bottom)
shows that the 10%
disadvantage
specified
in the
mortalities
was enough to drive
the p gene from 50% of
the gene pool to nearly extinct.
—————————————
A Few Instructive Simulations
The following
simulations will help
you learn population genetics,
particularly how genetic systems
change over time under various
assumptions about survival
and reproduction.
By adjusting
those parameters,
you can run scenarios about
anything you want, so please use
these suggestions just to get you
started. After that, be my guest.
Let your imagination
be your guide.
The model
is especially helpful in
understanding the population
genetics of Sickle Cell Anemia and other
inherited ailments, especially as they vary
among ecologically different environments.
The model is simple and grossly simplifies
enormously complex realities, but you’ll
be amazed to discover that you
can model those things.
Before
you run the model
under any set of parameters,
any time you run it, STOP! Imagine
the p, q, pp, pq, and qq curves
changing, generation by
generation, over 50
generations, the
shapes of
the curves.
Based on
your understanding of
the genetic and ecological system
you define and the selection regime you
specify, and mindful of what you want to learn
by it, what do you imagine will happen? You
don’t need calculations for this. It’s not
about math but understanding. Just
imagine the curves and see
what happens.
If you
don’t know for
sure, take a guess and
sooner than you think, two
things will happen. Your guesses
will become more accurate, more
of the time, as you home in on under-
standing of population genetics and
natural selection. As your under-
standing grows, so will your
appreciation of what you
don’t yet know.
You will discover
things you still need to learn
about genetics, population genetics,
and ecology. Together with your
imagination, the model will help you
find and learn them. Playing with
the model is a good way to find
out what you need
to study.
Simulations to run
Selection against
a lethal recessive allele
at various intensities.
Selection against
a lethal dominant allele
at various intensities.
Heterozygote superiority,
or selection against both homozygotes,
at various intensities.
Heterozygote inferiority,
or selection against heterozygotes,
at various intensities.
STOP!
After
you run the model,
each time you run it, STOP!
and think about what just happened.
Look at the curves. See if you can explain
to yourself how they came out that way, whether
you imagined it correctly or not. You’ll be
explaining these kinds of things to me
sooner than you think anyway,
so you may as well start by
explaining them to
yourself.
Learn
everything
you can learn
from each run, then
test what you learned by
running it a different way
and predicting the result.
—————-
Setting up a
lethal recessive simulation.
A population begins
at genotype frequencies
25% pp, 50% pq, and 25% qq.
All individuals of genotype qq die
before reaching reproductive age
(lethal recessive) and all individuals of
genotypes pp and pq survive and reproduce.
What are the genotype
and gene frequencies after 50 generations
of this kind and degree of selection?
Starting Frequencies
pp = 0.25
pq = 0.50
qq = 0.25
p = 0.50
q = 0.50
or any other frequencies you want.
Your question is what happens
and the same sort of thing
should happen regardless
of where you start, but
test this claim,
though; it could
be a trick.)
Mortalities
ppMort = 0.0
pqMort = 0.0
qqMort = 1.0
With those
starting frequencies and mortalities,
the model generates these frequencies
after 50 generations.
pp = 0.9619
pq = 0.0377
qq = 0.0004
p = 0.9808
q = 0.0192
This handout
and the model itself
evolved greatly over the years,
if only to keep up with technology.
It is at least 13 years out of date in 2019.
The suggestions
I give in this handout about how
to use the model as a learning tool, especially
about intentionally using it as a way to detect weaknesses
in understanding and home in on and repair them,
directly expresses how I suggest studying
in general in
First and Last Words from the
Trip Director.
History of the model.
Before 1974 my students did
Hardy-Weinberg calculations
with hand-held pocket calculators.
Needless to say, it was a long, tedious,
error-prone process to run it that
way, so the model was much
less useful to them than
what came later.
******
My students
and I used 2 Sharp EL-515
Solar-Powered calculators for 30
years at UBC and I’m still using both of them
in 2019! Unless those calculators can’t subtract,
I’ve been using them for 45 years and they’re
still going strong. I wonder how long an
abacus would last under the
abuse they’ve seen.
******
I wrote my
first H-W computer model in
Fortran in 1974, to run on the first Unix
machine in Canada, a DEC 11/45 intended only
for research. I brought small groups of first year
students into our tiny Zoology Data Centre to run
simulations, sometimes late at night. They told me what
parameters to enter, I entered them, and the results
came out on a big, noisy, typewriter-style printer
with big paper. When the PC revolution hit in
1978 I rewrote the model in Apple Basic and
Apple Pascal and brought students into
my lab (again intended only for
research) to do their
modeling.
Few students
had their own computers that
early and the model kept evolving
to keep up. Someone wrote it in Fortran
again for PCs and one in C ran on
bigger computers at UBC. When enough
students had access to computers one
of my graduate students wrote it in
Excel and students ran it as
much as they wanted
at home.
As soon
as they could do that
the model mushroomed in value
and became very useful! Now, after
45 years, anyone in the world who has
Excel and wants to understand how
natural selection operates on
populations of organisms
can run it.
A quick Google search shows
lots of similar programs are available.
I didn’t try any of them, but some are sure to be
easier to use, not require Excel, include more features,
and have better graphics than this model, but the point
of this story is not about the model anyway. It’s about
how I think about teaching and how I’ve lived it.
Edited May 2022